VECTORES Y GEOMETRÍA ANALÍTICA EN EL ESPACIO
FUNCIONES IMPLÍCITAS:
*En R^2: f(x,y)=0
Existen una o mas funciones
y=f1(x) y=f2(x)
x=g1(x) x=g2(x)
x=g1(x) x=g2(x)
Geográficamente representan una CURVA en el plano(R^2)
SISTEMAS DE FUNCIONES IMPLÍCITAS:
f(x,y)=0
g(x,y)=0
El sistema representa la intersección de las curvas generando uno o mas puntos
*En R^3: f(x,y,z)=0
z=f1(x,y) ; z=f2(x,y)...y=g1(x,z) ; y=g2(x,z)...x=h1(y,z) ; x=h2(y,z).
Geométricamente las funciones implícitas representan una SUPERFICIE en el espacio.
Ejemplo:
x^2+y^2+z^2-25=0 f(x,y,z)=0
x^2+y^2+z^2=25
Ecuación Superficie Esfera C(0,0,0) ; r=5
z=f1(x,y) ; z=f2(x,y)...y=g1(x,z) ; y=g2(x,z)...x=h1(y,z) ; x=h2(y,z).
Geométricamente las funciones implícitas representan una SUPERFICIE en el espacio.
Ejemplo:
x^2+y^2+z^2-25=0 f(x,y,z)=0
x^2+y^2+z^2=25
Ecuación Superficie Esfera C(0,0,0) ; r=5
z=√25-x^2-y^2 ; z=-√25-x^2-y^2
y=√25-x^2-z^2 ; y=-√25-x^2-z^2
x=√25-y^2-z^2 ; x=-√25-y^2-z^2
Positivo Negativo
f(x,y)=0
Representa una superficie con generatriz paralela al eje "z"
g(x,z)=0
Representa una superficie con generatriz paralela al eje "y"
h(y,z)=0
Representa un superficie con generatriz paralela al eje"x"
f(x,y,z=0
g(x,y,z)=0
La intersección de las superficies que representa cada función implícita genera CURVAS
ECUACIONES DE LA RECTA EN EL ESPACIO
*DADO UN PUNTO Y EL VECTOR DIRECTOR DE LA RECTADatos:
Dados esto datos la ecuación vectorial de la recta L es:
r= ro + tâ Ecuación Vectorial de la recta
----------------------------------------------------------
----------------------------------------------------------
x=xo+tl Ecuaciones
y=yo+tm Paramétricas de la
z=zo+tn Recta
----------------------------------------------------------
x-xo/l = y-yo/m = z-zo/n Ecuación Cartesiana o Canónica de la recta
*DADOS DOS PUNTOS

Datos:
y=yo+tm Paramétricas de la
z=zo+tn Recta
----------------------------------------------------------
x-xo/l = y-yo/m = z-zo/n Ecuación Cartesiana o Canónica de la recta
*DADOS DOS PUNTOS

Datos:
M1(x1,y1,z1)
M2(x2,y2,z2)
M2(x2,y2,z2)
Dados esto datos la ecuación vectorial entre dos puntos es:
r=r1+t(r2-r1) Ecuación Vectorial de la recta
--------------------------------------------------------------------------------------------------------------------------
x=x1+t(x2-x1) Ecuaciones
y=y1+t(y2-y1) Paramétricas de la
z=z1+t(z2-z1) Recta
--------------------------------------------------------------------------------------------------------------------------
x-x1/x2-x1 = y-y1/y2-y1 = z-z1/z2-z1 Ecuación Cartesiana o Canónica de la recta
Datos:
Mo(xo,yo,zo)
r=r1+t(r2-r1) Ecuación Vectorial de la recta
--------------------------------------------------------------------------------------------------------------------------
x=x1+t(x2-x1) Ecuaciones
y=y1+t(y2-y1) Paramétricas de la
z=z1+t(z2-z1) Recta
--------------------------------------------------------------------------------------------------------------------------
x-x1/x2-x1 = y-y1/y2-y1 = z-z1/z2-z1 Ecuación Cartesiana o Canónica de la recta
ECUACIONES DEL PLANO EN EL ESPACIO
*ECUACIÓN DEL PLANO DADO UN PUNTO Y EL VECTOR NORMAL AL PLANODatos:
Mo(xo,yo,zo)
r=(x,y,z)
ro=(xo,yo,zo)
Dados estos datos la ecuación vectorial entre dos puntos es:
Dados estos datos la ecuación vectorial entre dos puntos es:
(r-ro)•n=0 Ecuación Vectorial del plano ---------------------------------------------------------------- Ax+By+Cz+D=0 Ecuación General del plano
*ECUACIONES INCOMPLETAS
i) Ax+By+Cz+D=0 ; Si C=0
Ax+By+D=0
Ecuación del plano con generatriz paralela al eje "z".
ii) Ax+By+Cz+D=0 ; Si B=0
Ax+Cz+D=0
Ecuación del plano con generatriz paralela al eje "y".
iii)Ax+By+Cz+D=0 ; Si A=0
By+Cz+D=0
Ecuación del plano con generatriz paralela al eje "x".
iv)Ax+By+Cz+D=0 ; Si A=0 y B=0
Cz+D=0 ==> z=-(D/C)
Ecuación del plano con generatriz paralela al plano "xoy"
v) Ax+By+Cz+D=0 ; Si A=0 y C=0
By+D=0
Ecuación del plano con generatriz paralela al plano "xoz"
vi)Ax+By+Cz+D=0 ; Si B=0 y C=0
Ax+D=0
Ecuación del plano con generatriz paralela al plano "yoz"
Ax+By+Cz=0
Ecuación del plano que pasa por (0,0,0)
*ECUACIÓN SEGMENTARIA DEL PLANO
Ax+By+Cz+D=0
Ax+By+Cz=-D
x/-(D/A)+x/-(D/B)+x/-(D/C)=1
a=-(D/A)
b=-(D/B)
c=-(D/C)
==> x/a + y/b +z/c =1 Ecuación Segementaria del plano
Ax+By+Cz+D=0
Ax+By+Cz=-D
x/-(D/A)+x/-(D/B)+x/-(D/C)=1
a=-(D/A)
b=-(D/B)
c=-(D/C)
==> x/a + y/b +z/c =1 Ecuación Segementaria del plano
*ECUACIÓN PLANO DADO TRES PUNTOS
Datos:
M1=r1=(x1,y1,z1)
M2=r2=(x2,y2,z2)
M3=r3=(x3,y3,z3)
Dados estos datos la ecuación vectorial entre tres puntos es:
(r-r1)•(r2-r1)x(r3-r1)=0 Ecuación del Plano dados tres puntos(producto mixto)
El producto mixto (o también conocido como triple producto escalar) es una operación entre tres vectores que combina el producto escalar con el producto vectorial para obtener un resultado un escalar.
*Si el producto mixto es igual a cero, entonces los tres vectores son COPLANARES.
*El producto mixto generalmente representa el volumen del paralelepípedo cuyas aristas son los tres vectores.
M2=r2=(x2,y2,z2)
M3=r3=(x3,y3,z3)
Dados estos datos la ecuación vectorial entre tres puntos es:
(r-r1)•(r2-r1)x(r3-r1)=0 Ecuación del Plano dados tres puntos(producto mixto)
El producto mixto (o también conocido como triple producto escalar) es una operación entre tres vectores que combina el producto escalar con el producto vectorial para obtener un resultado un escalar.
*Si el producto mixto es igual a cero, entonces los tres vectores son COPLANARES.
*El producto mixto generalmente representa el volumen del paralelepípedo cuyas aristas son los tres vectores.
* EL VOLUMEN: C.(AxB) u^3
*EL ANGULO ENTRE DOS PLANOS:
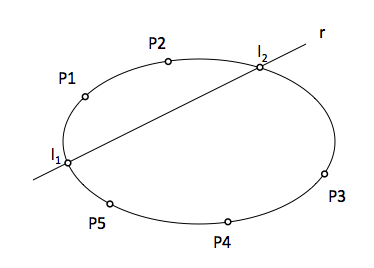
Si r viene definida por sus ecuaciones implícitas:

la ecuación del haz de planos de eje r viene dada por la igualdad:
Si dividimos por λ y hacemos , la ecuación del haz resulta:
, la ecuación del haz resulta:


la ecuación del haz de planos de eje r viene dada por la igualdad:
Si dividimos por λ y hacemos
 , la ecuación del haz resulta:
, la ecuación del haz resulta: 
DISTANCIA DE UN PUNTO A UN PLANO
La distancia de un punto, P, a un plano, π, es la menor de la distancia desde el punto a los infinitos puntos del plano. Esta distancia corresponde a la perpendicular trazada desde el punto al plano.

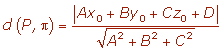
ECUACIÓN VECTORIAL DE LA ESFERA
Datos:
c(x0,y0,z0)
radio: R
Dados estos datos la ecuación vectorial de la esfera es:
(r-r0)^2=R^2 Ecuación Vectorial de la Esfera con c(x0,y0,z0) y radio R
----------------------------------------------------------------------------------------------
(x-x0)^2+(y-y0)^2+(z-z0)^2=R^2 Ecuación Cartesiana de la Esfera
CILINDROS Y SUPERFICIES CUADRÁTICAS
*CILINDRO
Superficie generada por las lineas rectas paralelas llamadas GENERATRICES que intersecan a una curva plana.
* Superficie z=x^2
i)generatriz paralela al eje y
ii)curva plana z=x^2 (plano xoz)
*Superficie y^2+z^2=1
i)generatriz paralela al eje xii)representa circunferencia
iii)y^2+z^2=circunferencia
c(0,0);R=1;(plano yoz)
*Superficie x=y
i)generatriz paralela al eje z
ii) y=x ; recta en el pano xoy
*CÚADRICAS
Son superficies que tienen por ecuación:
Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0 donde:
A,B,C,...,J son constantes, pero que si la superficie se traslada o se rota puede toma valores de cero.
*ANÁLISIS GRÁFICO DE LAS SUPERFICIES
Para realizar una gráfica de las superficies a continuación puntualizamos los pasos a seguir:
I) Intersección con los ejes coordenados
i) Con el eje OX
ii) Con el eje OY
iii) Con el eje OZ
II) Intersección con los planos coordenados
i) Con el plano XOY
ii) Con el plano XOZ
iii) Con el plano YOZ
III) Intersección con los planos perpendiculares a los planos coordenados
i) Con los planos perpendiculares al plano XOY
ii) Con los planos perpendiculares al plano XOZ
iii) Con los planos perpendiculares al plano YOZ
IV) Representación Gráfica
FUNCIONES VECTORIALES DE VARIABLE REAL
F: I c R -> R^n
t -> F(t) = (f1(t),f2(t);...fn(t))
donde:
Cada fi(t) es una función de I en R
*El dominio de F(t) es:
DF= Df1∩Df2∩...∩Dfn
*El rango o recorrido de F(t) es:
RF=Rf1∪Rf2∪...∪Rfn
Ejemplo:
f1(t)=t^2+5 --> Df1=R
f2(t)=sen(t) --> Df2=R
f3(t)=1-t --> Df3=R
∴ DF=R
*Si F toma valores en R^3
se puede escribir: F(t)=(x(y),y(t),z(t)) ó F(t)=x(t)i+y(t)j+z(t)k
donde: x(t),y(t) y z(t) se denominan las componentes de F(t).
Se puede obtener:
x(t)=f1(t)
y(t)=f2(t) t∈R
z(t)=f3(t)
Se denominan Ecuaciones Paramétricas de F(t) y t se deomina parámetro.
*El gráfico de una F(t)=(x(y),y(t),z(t)) es una curva c en el espacio, llamada CURVA ALBEADA.
*El gráfico de una F(t)=(x(y),y(t)) es una CURVA PLANA.
OBSERVACIÓN: Si es posible eliminar el parámetro "t" se obtiene la ECUACIÓN CARTESIANA de la curva c.
OPERACIONES DE FUNCIONES VECTORIALES
LIMITES Y CONTINUIDAD
Dado la función:
F: I c R -> R^n
t -> F(t) = (f1(t),f2(t);...fn(t))
y si A=(a1,a2,...,an) entonces:
lim F(t) = A <---------> lim fi(t)=ai
t->to t->to
*El límite de F(t) existe ssi el límite de cada fi existe, en caso contratio si solo una de las fi no tiene limite, entonces se concluye que: no existe lim F(t)
t->to
*CONTINUIDAD
Sea F: I c R -> R^n
t -> F(t) = (f1(t),f2(t);...fn(t))
Se dice que F(t) es continua en to, si se cumple:
lim F(t)=F(to)
t->to
i)∃ F(t0)
ii)∃ lim F(t)
t->to
iii) lim F(t) = F(to)
t->to
DERIVACIÓN E INTEGRACIÓN
Dada una función vectorial F: I --> R^n, donde I c R y sea to ∈ I, se dice que F es derivable en to, si existe:
lim F(to+h)-F(to)/h
h->0
Notación
La derivada de F(t), se denota por:
F'(to)=DtF(to)=dF(to)/dt
Por tanto:
F'(to) = lim F(to+h)-F(to)/h
h->0
Propiedades
Interpretación Geométrica:
INTEGRACIÓN
Sea F: I --> R^n ; I c R ; entonces:
*Para integrar F(t) se integra cada uno de sus componentes
*La integral de F(t) existe si cada una de las integrales de fi(t) existen.
LONGITUD DE ARCO Y CURVA
*La longitud de una curva plana con representación paramétrica; x=f(t), y=g(t), a<=t<=b, se define como el limite de las longitudes de polígonos inscritos y en el caso donde f' y g' son continuas: 
Longitud de Arco Curva Plana
F(t)=(f(t),g(t),h(t))
a<=t<=b, donde f',g' y h' son continuas
Longitud de Arco Curva 3D
*Una curva c, puede ser representada por mas de una parametrización, por ejemplo:
r(t)=(t,t^2,t^3); 1<=t<=2
se podría representar por:
r(u)=(e^u,e^2u,e^3u); 0<=u<=ln2
donde t=e^u
En general si c es una curva suave por partes,dada por:
r(t)=f(t)i+g(t)j+h(t)k ; a<=t<=b
donde r'(t) es continua y c es recorrida exactamente una vez cuando t se incrementa desde "a" hasta "b", entonces:
TRIEDRO MOVIL
r(t)=(f(t),g(t),h(t))
r(s)=(Φ(t),φ(t),γ(t))
r'(t)=(f'(t),g'(t),h'(t))
r'(t)= T Vector TangenteB=r'(t) x r''(t) Vector Binormal
N=B x T Vector Normal Principal
eje OX ==>RT i ==> T=T/|T|
eje OY ==>RN j ==> N=N/|N|
eje OZ ==>RB k ==> B=B/|B|
*Plano osculador T^N
*Plano normal B^N
*Plano rectificante T^B
PLANO OSCULADOR (PO)
Mo(xo,yo,zo) ; n=B=(B1,B2,B3)
(r-ro)•B=0
(x-xo;y-yo,z-zo)•(B1,B2,B3)=0
B1(x-xo)+B2(y-yo)+B3(z-zo)=0
PLANO NORMAL (PNP)
Mo(xo,yo,zo) ; n=T=(T1,T2,T3)
(r-ro)•T=0
T1(x-xo)+T2(y-yo)+T3(z-zo)=0
PLANO RECTIFICANTE (PR)
Mo(xo,yo,zo) ; n=N=(N1,N2,N3)
(r-ro)•N=0
N1(x-xo)+N2(y-yo)+N3(z-zo)=0
RECTA TANGENTE (RT)
Mo(xo,yo,zo) ; a=T=(T1,T2,T3)
r=ro+ta
r=ro+tT
x=xo+tT1
y=yo+tT2
z=zo+tT3
RECTA NORMAL (RN)
Mo(xo,yo,zo) ; a=N=(N1,N2,N3)
x-xo/N1 = y-yo/N2 = z-zo/N3
RECTA BINOMIAL (RB)
Mo(xo,yo,zo) ; a=B=(B1,B2,B3)
x-xo/B1 = y-yo/B2 = z-zo/B3
































No hay comentarios:
Publicar un comentario