CLASES DE CURVATURA
*CURVATURA DE FLEXIÓN(K)
Dada una curva regular F(t) se puede reparametrizar, de manera que la longitud de la curva entre dos puntosa y b,coincida con la longitud del intervalo con origen en a y extremo en b; en este caso se dice que la curva está parametrizada por la longitud de arco,que llamamos.
En este caso el vector tangente siempre es unitario.Se define la curvatura k como la variación del vector tangente respecto a la longitud de arco.
La curvatura viene a medir como se “tuerce” la curva respecto de su longitud. Esta definición es bastante
intuitiva,
pero no es fácil de calcular. Para curvas, no necesariamente parametrizadas por el arco, se puede calcular
como
Ejemplo gráfico:
Nota Importante:
*Se llama radio de curvatura de flexión al inverso de la curvatura de flexión
*La curvatura de flexión es la razón de cambio de dirección del vector T de un punto a otro
*CURVATURA DE TORSIÓN(T)
La torsión nos indica el alejamiento o acercamiento de la curva a un plano osculador
Las curvaturas de Flexión y Torsión se calculan también
FUNCIONES ESCALARES DE VARIAS VARIABLES
Una función escalar, también llamada función real de varias variables ( o de variable múltiple) es una aplicación que representamos por f:A⊆Rn⇒R (x1,x2,...,xn)⇒z=f(x1,x2,...,xn) , donde el conjunto A⊆Rn se llama dominio de f, se representa por A=Dom(f)=Domf.
El dominio de f, es el conjunto de los elementos de Rn que tienen imagen mediante f, es decir: A=Domf={(x1,x2,...,xn)∈Rn/∃f(x1,x2,...,xn)}
Llamamos imagen de la función f al conjunto de los números reales que tienen correspondencia con algún elemento del dominio, se representa por
Im(f).
Im(f)={z∈R/∃(x1,x2,...,xn)∈A⊆Rn verificandoz=f(x1,x2,...,xn)}
Descriptores: Funciones de varias variables
Funciones
Ejemplo:
La función f:A⊆R2⟶R definida por f(x,y)=+√x2y. Es una función escalar de dos variables. Determinar su dominio y su imagen.
*Dominio de la función.
∃f(x,y)⇔x2y≥0⇔y≥0⇒Dom(f)={(x,y)∈R2/y≥0}
*Imagen de la función.
x2y≥0⇒+√x2y≥0⇒Im(f)=[0,+∞[⊂R
*GRÁFICOS
Si f es una función de dos variables con dominio D entonces la gráfica de f es el conjunto de todos los puntos (x,y,z) en R3 tal que z=f(x,y), siendo (x,y) pertence R
CURVAS DE NIVEL
*Las curvas de nivel de una función f(x,y) serán las curvas cuyas ecuaciones son f(x,y)= k, donde k es una constante en el rango.
*Las curvas de nivel sirven para realizar la topología de una región.
*Si la función f(x,y) representada:
i)La función de la temperatura, las curvas de nivel se denominan ISOTERMAS.
ii)La función de la potenciación, las curvas de nivel se denominan EQUIPOS TENCIALES.
iii)La función de la Presión las curvas de nivel se denominan ISOBARAS.
Si las curvas de nivel se representan en 3D, entonces se denominan curvas de contorno
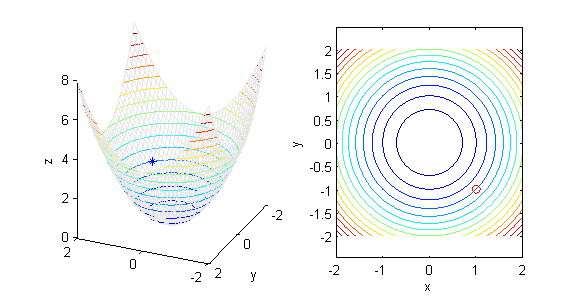
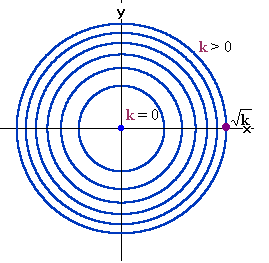
Ejemplo:
Consideremos la función z = x2 + y2. Tomando k > 0, la curva de nivel correspondiente a z = k es la circunferencia x2 + y2 = k y tomando k = 0 la curva de nivel corresponde a la descrita por los puntos (x, y) tales que x2 + y2 = 0 (que corresponde únicamente al punto (0, 0))
LIMITES Y CONTINUIDAD
Sea f: R2==>R
(x,y)==>z=f(x,y)
Una función de dos variables, cuyo dominio D contiene entre otros, puntos arbitrariamente cercanos a (a,b). Entonces el limite de f(x,y) cuando (x,y) tiende a (a,b), por lo que se escribe:
Lim f(x,y)=L <---> para todo E>0 ; exista d>0 si (x,y) pertenece R y
(x,y)-->(a,b)
*otras formas de detonación son:
f(x,y)==> L cuando(x,y) ==>(xo,yo)
Ejemplo:
Entorno: D:|(x,y)-(a,b)|<d
|(x-a;y-b|<d
(x-a)^2+(y-b)^2<d^2 ==> Ec. de c(a,b) y R=d
Si para cada E>0 existe un d>0 tal que
Gráficamente, esta definición de límite implica que para cualquier punto (x,y) no es igual (Xo,Yo) en el disco de radio d, el v f(x,y) esta entre L+E YL-E.
El valor de la definición anterior se refiere sólo a la distancia entre (x, y) y (Xo,Yo) . No habla a la dirección de aproximación. Por eso, si el límite existe, entonces f(x,y) debe aproximarse a mismo límite, sin importar la forma en que (x, y) se aproxime a (Xo,Yo) . Así pues, si podemos encontrar dos diferentes trayectorias de acercamiento a lo largo de las cuales f(x,y) tiene distintos límites, entonces se concluye que el límite no existe.
Si f(x,y) ---->L1 conforme (x, y)----> (Xo,Yo) a lo largo de una trayectoria C1 y f(x,y)--->L2 conforme x, y)----> (Xo,Yo a lo largo de una trayectoria C2 ,donde L1 NO ES IGUAL A L2, entonces el límite no existe.
Notas Importantes:
*Para las funciones de dos variables, el domino es una parte o todo el plano xoy, por tanto existen infinitos caminos o trayectorias de acercamiento.
*Si por dos caminos diferentes el valor del limite toma diferente valor, podemos concluir que el limite no existe
*Si por dos o mas caminos diferentes el limite toma el mismo valor "L", se supone que el limite existe y se debe procede a demostrarlo
*CONTINUIDAD
Para demostrar que f(x,y) es continua en (a,b) entonces debe cumplirse que:
i) Existe f(a,b)
ii)Existe
Se pueden presentar dos tipos de discontinuidad:
Evitable
Se redefine la función para obligarle a que cumpla la condición
Inevitable
Si no existe el límite de la función
DERIVADAS PARCIALES
Derivada parcial de una función de varias variables.
Sea una función de dos variables z = f(x, y), se definen las derivadas parciales:
(Una definición obvia si la comparamos con la derivada de una función de una variable)
Para la derivada de z "respecto de x" consideramos a la variable "y" como si fuera una constante, mientras que al hacer la derivada de z "respecto de y" consideramos a la variable "x" como si fuera constante.
Para ello recordemos que la derivada de la función z = eu es: z’ = u’ . eu , siendo u en nuestro caso: x2 + y2 , entonces la derivada de u respecto x es 2x (con la yconstante), mientras que la derivada de u respecto y es 2y (con la x constante). Así tenemos:
Otras formas de expresar la derivada de la función z = f(x,y) con respecto a x son:
mientras que para expresar la derivada de la función z = f(x,y) con respecto a y :
Esta definición de derivada se extiende a funciones de tres o más variables, por ejemplo, para una función de tres variables w = f(x,y,z) sus tres derivadas parciales son:
en cada una de ellas se consideran constantes los dos parámetros distintos a los que se realiza la derivada.
*DIFERENCIAL DE VARIAS VARIABLES
Sea una función de dos variables z = f(x, y), se define la diferencial de esta función como:
Geométricamente hay que interpretar las diferenciales como "incrementos infinitesimales".
Como ejemplo, expresemos la diferencial de la función: , ya que hemos realizado anteriormente las dos derivadas parciales:
, ya que hemos realizado anteriormente las dos derivadas parciales:
 , ya que hemos realizado anteriormente las dos derivadas parciales:
, ya que hemos realizado anteriormente las dos derivadas parciales:
Tanto en las derivadas como en las diferenciales, se suele hablar de valores en un punto P(a, b), para ello se sustituye en ellas el valor de x por a, y el valor de y por b. Por ejemplo, las derivadas y la diferencial en el punto P(1, 2) se calculan sustituyendo x=1, y=2.
y la diferencial en ese punto:
*DERIVADAS PARCIALES DE SEGUNDO ORDEN
Sea una función de dos variables z = f(x, y). En principio tenemos cuatro (22) derivadas de segundo orden
(se debe leer "derivada segunda de z respecto de x dos veces", "derivada segunda de z respecto de x-y", etc.) Estas derivadas vienen definidas de la siguiente manera:
Las derivadas son llamadas "derivadas mixtas", obsérvese en el ejemplo cómo estas derivadas son iguales, lo cual no es una coincidencia sino el resultado de un teorema que vamos a pasar a ver.
son llamadas "derivadas mixtas", obsérvese en el ejemplo cómo estas derivadas son iguales, lo cual no es una coincidencia sino el resultado de un teorema que vamos a pasar a ver.
 son llamadas "derivadas mixtas", obsérvese en el ejemplo cómo estas derivadas son iguales, lo cual no es una coincidencia sino el resultado de un teorema que vamos a pasar a ver.
son llamadas "derivadas mixtas", obsérvese en el ejemplo cómo estas derivadas son iguales, lo cual no es una coincidencia sino el resultado de un teorema que vamos a pasar a ver.
*DIFERENCIAL SEGUNDA DE UN FUNCIÓN Z=F(X,Y)
Sea z = f(x,y) una función de dos variables. Entonces la diferencial segunda de z, d2z, es la diferencial de la diferencial, esto es, d(dz), la cual se puede expresar así:
que teniendo en cuenta la igualdad (en general) de las derivadas mixtas, puede expresarse:
En nuestro ejemplo tendríamos:
NOTA:
* Podemos hallar la diferencial de z = f(x,y) en un punto específico, digámos P(a,b), sin más que sustituir las x por a, y las y por b.
Hallemos, para la función z de nuestro ejemplo, la diferencial de z en el punto P(1,2):
TEOREMA DE CLAIRAUT
Si f(x,y) y sus derivadas parciales fxy, fyx están definidas en un disco D que contiene al punto (a,b) y son todas continuas en (a,b), entonces
fxy (a,b) = fyx (a,b)
Se tienen 2^n derivadas de orden "n"
Se tienen 3^n derivadas de orden "n" en R^3
REGLA DE LA CADENA
Caso de una variable independiente:
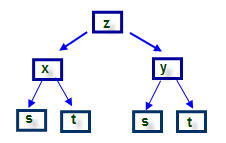
Sea z=F(x,y) una función suave, es decir, con derivadas parciales continuas y supongamos que tanto x como y son funciones de un parámetro t y ambas tienen derivadas respecto de t. Entonces z=F(x(t),y(t)) es una función compuesta. Un cambio en t afectará a las variables x e y, por lo tanto se producirá un cambio en z. Es razonable preguntarse por la razón de cambio de z respecto a t. Esta derivada puede obtenerse:
dz dt = ∂ z ∂ x . dx dt + ∂ z ∂ y . dy dt
*DERIVACIÓN PARCIAL IMPLÍCITA
En la matemática la derivada parcial implícita corresponde a una función que tiene diversas variables, en este caso es una derivada con respecto a una de las variables manteniendo todas las otras como constantes. Las derivadas parciales implícitas con usadas en los cálculos de vectoriales y geometría diferencial. La derivada parcial de una cualquier función f respecto a la variables x puede ser representada como:
Al completar la derivada se obtiene la una expresión que nos permite encontrar la pendiente de una recta tangente de una función en un punto dado.
EJEMPLOS:
*PLANO TANGENTE Y RECTA NORMAL A UN SUPERFICIE
Se llama plano tangente a una superficie en un punto P de la misma, al plano que contiene todas las tangentes a las curvas trazadas sobre la superficie por el punto P.
Se llama recta normal a una superficie a la recta que pasa por un punto P y es perpendicular al plano tangente.
Si la superficie está definida de manera implícita por la ecuación F(x,y,z)=0, entonces la ecuación del plano tangente en un punto  de la superficie viene definido por la ecuación:
de la superficie viene definido por la ecuación:
 de la superficie viene definido por la ecuación:
de la superficie viene definido por la ecuación:
y la recta normal por:
Si la ecuación de la superficie está definida de manera explícita z = f(x,y) entonces la ecuación del plano tangente en el punto viene definida por:
y la ecuación de la recta normal:
La ecuación del plano tangente se puede utilizar para calcular el valor aproximado de una función. Gráficamente significa medir el valor de la función sobre el plano tangente y no sobre la superficie.
*DERIVADA DIRECCIONAL Y VECTOR GRADIENTE
Se llaman derivadas direccional de la función z = f(x,y) en un punto P(x,y) en el sentido del vector  si el siguiente limite si existe y es finito.
si el siguiente limite si existe y es finito.
 si el siguiente limite si existe y es finito.
si el siguiente limite si existe y es finito.
Para calcular este límite se toma el vector unitario  de la dirección del vector
de la dirección del vector  dividiéndolo por su módulo). Llamamos t a la longitud del vector
dividiéndolo por su módulo). Llamamos t a la longitud del vector  ,es decir
,es decir , con lo cual
, con lo cual  , de donde
, de donde  y el límite se reduce a la única variable t
y el límite se reduce a la única variable t
 de la dirección del vector
de la dirección del vector  dividiéndolo por su módulo). Llamamos t a la longitud del vector
dividiéndolo por su módulo). Llamamos t a la longitud del vector  ,es decir
,es decir , con lo cual
, con lo cual  , de donde
, de donde  y el límite se reduce a la única variable t
y el límite se reduce a la única variable t
Si la función f(x, y) es diferenciable, entonces la derivada direccional s
e calcula por la fórmula:
(es decir la suma de los productos de las parciales por las componentes del vector unitario)Si la función es de tres variables z=f(x, y, z) la derivada direccional se calcula de manera análoga:
(Las parciales habrá que calcularlas en el punto correspondiente. Las componentes del vector unitario coinciden con los cosenos directores del vector director. Si la función no es diferenciable esta fórmula no es válida y hay que calcular el límite anterior).
Se llama gradiente de una función z = f(x, y) en un punto P(x, y) al vector que sale del punto P y sus componentes son las derivadas parciales de la función en dicho punto
La derivada direccional se puede obtener como el producto escalar del gradiente por el vector unitario (si la función es diferenciable)
El gradiente indica el sentido de crecimiento más rápido de una función en un punto dado. La derivada direccional tiene su valor máximo en el sentido del gradiente y coincide con su módulo
Si la función es de tres variables u = f(x, y, z) el gradiente se define de forma análoga:






















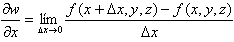


























No hay comentarios:
Publicar un comentario